







Computer Algebra
MSE
Matthias Meyer
Exam summary
Switzerland
20.1.2023
Summary created by Matthias Meyer. Note there might be errors!
Some parts are also available on the following webpage.
Collocation = All measurement points are represented by a function, for example a polynomial. The polynomial
results in a linear equation system with a degree of n+1.
One way to solve this is by searching a polynomial formula as can be seen below. (It would also possible to generate a function by connecting the different data points with a straight line. ⇒ On a Computer this would take a lot of computational effort, since one would have a lot of if and else statements)
To get the solution of this polynomial, one has to solve the following equation system:
As one can see, this equation system gets really large and could be difficult to be solved on a microcontroller. But there exists a nice algorithm which makes solving this system easier, called Aitken-Neville recursion which divides the huge equation system in little parts.
The formula above shows how the global interpolating polynomial is combined from the partial interpolation polynomials p0,1,2,…,n−1(x)and p1,2,…,n−1,n(x). On this partial interpolation polynomials, one can again apply the formula until one ends up with only two datapoints.
Since the calculation with the Aitken-Neville recursion is quite tedious. Newton came up with another basis polynomial πk(x) with k= 0,1,2,...,n (Aitken-Neville recursion used (1,x1,x2,....,xm)
| (1) |
Which results in the final polynomial which can be seen in Equation 2
| (2) |
When one now writes the equation system one sees that this system is much easier to solve:
When one also applies the Aitken-Neville recursion it even get easier and independent of the order, since one just calculates divided differences. Below one can see the calculation of the first ak terms.
Where y is called the divided difference.
When the points have the same distance to each other, the formula gets even easier:
Given is the following dataset:
Calculate the collocation polynomial.
One can do the calculation the following way:
and therefore get the following result for the given data points:
According to Equation 2 one gets then the following result:
It does not depend on which data point one uses first and which one as last element. The resulting formula might look different (different ak coefficients, but the last one is the same), but the result is exactly the same. Furthermore, the data points must not have the same spacing.
With a lot of data point the runge phenomenon occurs (oscillations with high frequencies and amplitudes towards the boundaries of the arguments range) To calculate the error which can be seen one can use the following formula:
Where ξ is a new data point. can also be substituted by ⇒C=
It is a newton polynomial with one more argument. is a higher order derivative which we do not know at the
moment. The formula can also be rewritten in Equation 3:
| (3) |
When generalizing it one can also write Equation 4
| (4) |
The model fucntion y(x) =sin(πx) has to be interpolated using the arguments x= 0;1;2 by a quadratic
polynomial p(x), what is the error at the position x=
Error = y(x) −p(x) =sin(πx) −
0+1(x−0)+1(x−0)(x−1)
To reduce the error mentioned above to a minimum one can use a chebyshev distribution of the arguments.
When the problem of collocation, which can be found on the following post is extended by the requirement that certain given values of derivatives of order 0 up to some higher order k of the model function y must be met at some of the arguments x0,x1,...,xn we end in an interpolation problem called osculation or Hermite interpolation. Furthermore note that one must use the modified newton polynomials as they can be seen in Equation 5, for the example provided there
We have railway track with the following points given:(0;0),(2;1),(4;2) and also its derivatives. Now we have to search a polynomial p2 which goes through point one and point two and fulfils it’s derivatives. So we have the following conditions: p2(2) =1,p2′(2) =1,p2′′(2) =0 and p2′(4) =0,p2(4) = 2,p2′′(4) =0
This lead to the following result: p2 =1 ·π0 +1 ·π1 + 0 ·π2 −π3 +
π4 when using the modified newton
polynomials as they can be seen in Equation 5.
| (5) |
The problem with this method it is that it is not guarateed to find a solution for this problem, when not all
derivatives are given. One then has to increase the order of the polynomial.
Error With Equation 4 the error is then:
The maximum error therefore is: ·
·
Compute two fourth-degree (!) polynomials, p1(x) and p2(x), meeting the constraints below:
and
Moreover, the two polynomials should meet smoothly at the point (2,1) without a crinkle (with a common tangential line) To solve this problem we introduce a new variable called a which defines the first derivative at point (2,1). When a is equal in both equations the meeting of the two polynomials is very smoothly. The first scheme looks like this:
Where
since p1 must be of order 4 se conclude that |F|= 0(!) and therefore a= 1
Now one can do the same thing for the next polynomial but a is this time known. When solving it one gets the following result:
The polynomial interpolation can also be used with a Multi-variate Polynomial Interpolation. Where the polynomial is represented by Equation 6.
| (6) |
p(x,y) p(0,0) =0,p(1,0) =1,p(0,1) = 0,p(1,1) = 0.5 Now lets calculate the first x row:
Now lets calculate the second x row:
And in step 3 we combine those two.
How many conditions are generally required
for a tri-linear polynomial interpolation
We have three dimensions and a linear polynomial ⇒ we have 8 basis functions (2 · 2 · 2) ⇒ 8 conditions that are required:
for a tri-cubic polynomial interpolation
We would need to define;
The Idea of the spline interpolation is that one does not interpolate the data with a high degree polynomial, but with multiple polynomials of lower degree. Due to that the runge phenomenon does not occur which occurs for high deggre interplations. When following this approach the transition of one spline ot the next must be considered. Normally one says that the derivative up ot an order n must be the same from one to the next spline. The drawback of this approach is that one needs a lot of storage, since one needs to store a lot of fucntions. The advantage is that it is easier to calculate, since the newton interpolation has a complexity of n2 whereas a cubic spline interpolation has a complexity of n.
A spline can be described with Equation 7
| (7) |
In natural splines the energy is minimized, therefore y0′′= 0 =yn′′
For natural spline c0 and cn are given by Equation 8
| (8) |
For cubic splines the a coefficients can be calculated according to Equation 9
| (9) |
The b coefficients can be calculated according to Equation 10
| (10) |
The d coefficients are given by Equation 11
| (11) |
| (12) |
Error Calculation for cubic splines with C2
| (13) |
| (14) |
Calculate the natural cubic spline-interpolation for a sine function sin(x) in the interval [0,π] according to the
points {0,,π}. Also calculate the maximum error.
From Equation 7 one knows that
Furthermore c0 = 0 (Equation 8) since we use natural splines and a0 =y0 = 0,a1 =y1 = 1 (Equation 9). From Equation 13 one can write down the following equations:
From Equation 10 one knows that
From Equation 11 one knows that
And finally from Equation 10 that:
The error can then be estimated with Equation 13.
The data below was generated by the sine function. In this example, the natural and clamped spline as well as the max error are calculated.
| (15) |
| (16) |
For the two examples above (natural and clamped) give maximum estimations for the following error
quantities ∣y(x) −S(x)∣, ∣y′(x) −S′(x)∣ and ∣y′′(x) −S′′(x)∣. The osculation error of a cubic spline can be
calculated with ?? and the osculation error of a periodic cubic spline () with
Equation 13.,
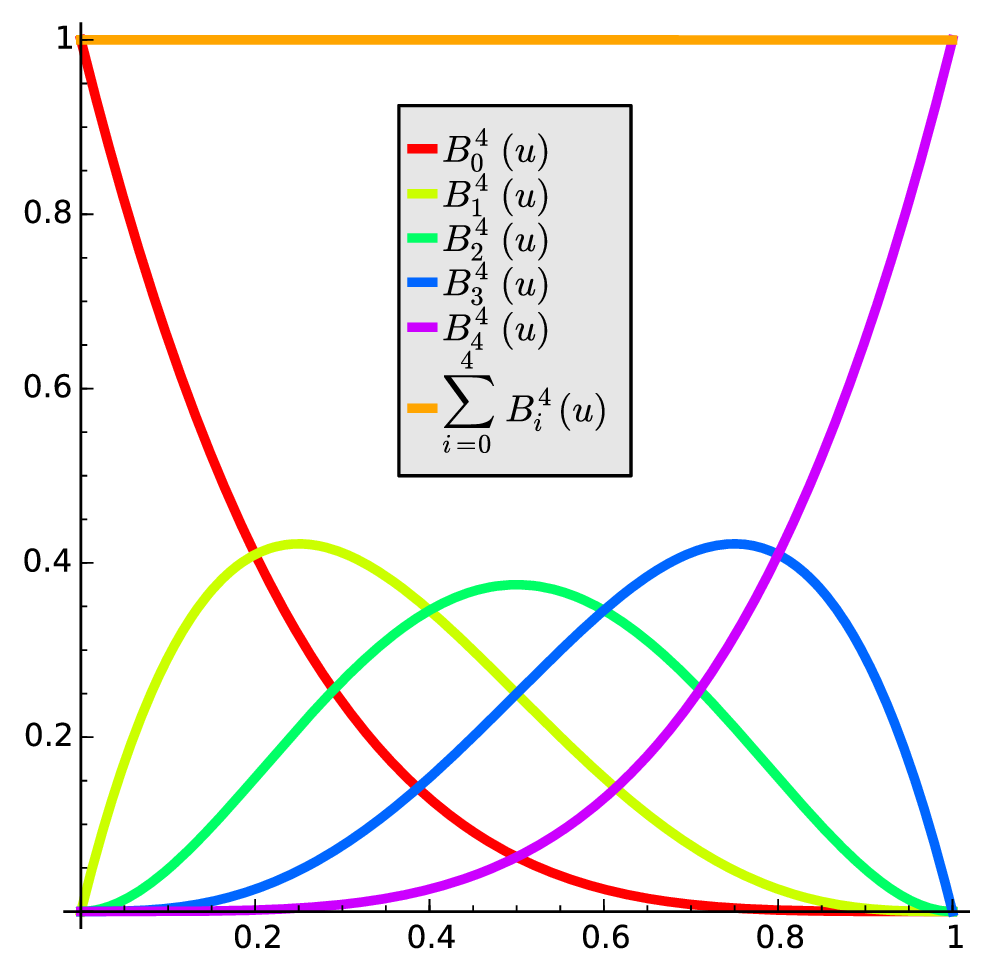
The bernstein-Bézier splines should give the same result as the cubic splines mentioned in the previous chapter. The difference is that one does not get a single formula in the end, but different data points. A good explanation can be found in the following video. But first of all to understand bézier curves/spline one must be familiar with Bernstein polynomials and therefore with the binomial coefficient (see also Equation 17)
| (17) |
Example: (For what can the binomial coefficients be used?) What is the fourth term of (3x− 4y)6 (note there is no zeroth term, therefore we subtract one in the equation blew)? The result can also be read from Figure 2.
Therefore, the fourth term is:
This is much easier than to really calculate the polynomial. An explanation can also be found in the following video
The bernstein polynomial is defined in Equation 18.
| (18) |
In Equation 18 one had an interval ∈ [0,1]. When our data is in another range like ∈ [a,b] one has to use Equation 19
| (19) |
Furthermore note that those polynomials look like one can see in Figure 3.
The polynomials relate to each other, as one can see in Equation 20.
| (20) |
A simple Bézier curve is defined with Equation 21. To get the idea also have a look at Figure 4.
| (21) |
Where:
The simple Bézier curves meet at common control points. Which is a continuity condition (C0), but often higher (smoothness) conditions are required (Ck-smooth). This condition is only met if and only if Equation 22 is given.
| (22) |
Writing out Equation 22 for C1 smoothness results in Equation 23, whereas C2 smoothness results in Equation 24 where one has to know that also Equation 23 C1 smoothness must be met.
| (23) |
| (24) |
The Bézier-curve is defined by the control points and the Bernstein polynomials. On each
spline one has n+1 control points.

The four points A= (0,0),B= (1,0),C= (2,3) and D= (2,4) are to be interpolated (joined) by composed
C1 Bernstein-Bézier splines: A and B are to be joined linearly (by a straight line), as well as C and
D.
Compute the missing C1 Bernstein-Bézier spline of minimal degree between B and C.
To solve the exercise one can use Equation 23. Where the first spline and the last one have two control points,
since it is a straight line ⇒n=1. The second spline has four conditions, since tow points must be met
and two derivatives, since it must be C1 smooth. Due to that n=3 ⇒ the degree is also 3 (also called
cubic).
The Casteljau recurrence is a similar idea as the neville-aitken. With this Idea a point on the Bézier curve can be calculated as a linear combination of two points on a Bézier curve of a lower degree.
Is (t) =∑
i=0nPi,jBi,n(t) t∈ [0,1] with the functions Qj defined (degree: n ), the following formulas turn
out:
Let’s do the same example as in subsubsection 5.2.5. Where the following four points are given:
Therefore Q0 = (0,0),Q1 =,… and hj=h=
. One now has to met the following requirements:
The solution of the linear system above gives us the following points:
When we now calculate the first spline we get the same result as before.
| (25) |
For the second spline we get the following:
| (26) |
Interpolation with the collocation methods often run into oscillation problems for (rather large) sets of measurement points. Furthermore, in most cases the measurements also contain some error points, which one does not want to represent in the graph. Due to that, an approximation (data points are not represented exactly any more) might be the preferred way to represent the data.
To find the best approximation, one must define what is a good and what is a bad approximation, which could be
with the following basic functions:
Note: Error = residuals ⇒ norm of residuals
Mathematically, the minimization of the squared errors is the easiest, therefore this one is most commonly used
(least square approximation) 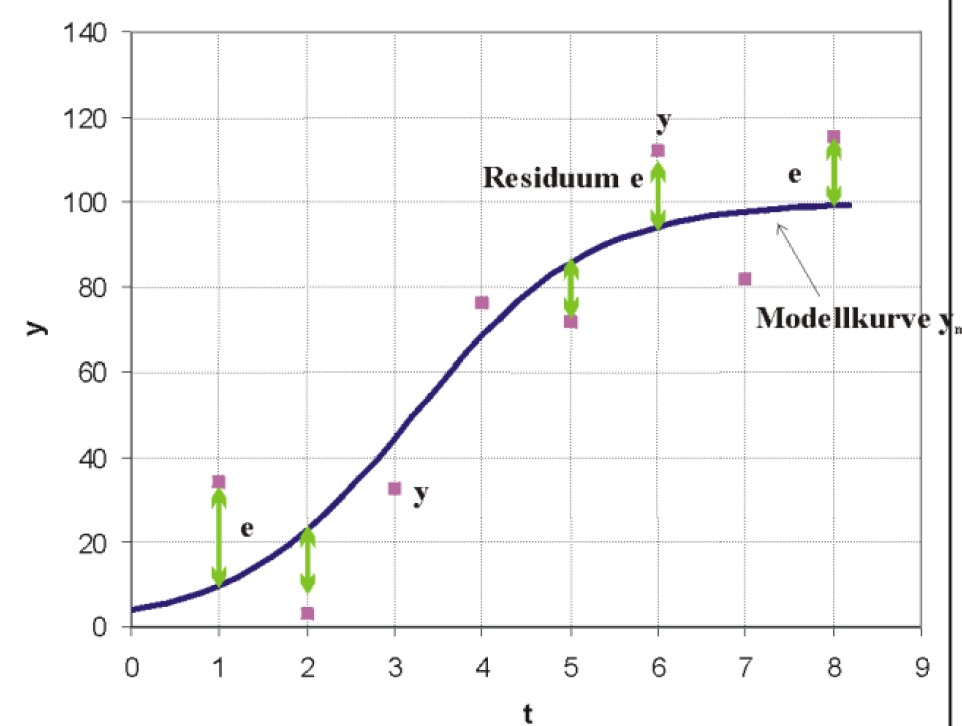
Figure 6: Data approximated by an error curve
The approximation function can be described with a set of basis functions, which we name here
g0,g1,…,gm=j=0,…,m. Note the basis functions are sometimes also called monomials. Furthermore we define
the following
With those variables one can create a equation in matrix notation form, as can be seen in Equation 27:
| (27) |
Since Equation 27 is normally overdetermined (m≪N) The error/residuals can be calculated with Equation 28 and the squared sum S of residuals with Equation 29. The goal is now to minimize S from Equation 29. This can be done with Equation 30, which is not derived in this post (for more information, search after orthogonal projection).
| (28) |
| (29) |
Lets assume one has the following points: {1,1},{2,2} and one wants to approximate those points by a polynomial of degree zero (m= 0) ⇒g0(x) = 1. Then one can write the term inside the square brackets as the following:
But as one can see one can not take the square of this term, therefore one has to multiply on both left sides with GT which has no effect on the end result, since one is only interested in the minimum.
When one squares the term above and says that GT·y and GT· G belong to each other, (are not separable) and
then takes furthermore the derivative, one gets the following result: 2 ·· (GT· G). When one sets
this term to zero since one is interested in the minimum and solves it after a one gets the result from
Equation 30.
| (30) |
A singular-value decomposition is one of the most widely used matrix operations in applied linear algebra.
Every Matrix G with the dimensions (N+ 1) × (m+ 1) can be decomposed as the triple product UDV T whereas U is an orthogonal (N +1) × (N +1) -matrix, D is a (N +1) × (m +1) diagonal matrix and V again is orthogonal with dimensions (m +1) × (m +1). When a matrix is orthogonal, the following applies: QTQ=QQT =I and QT =Q−1. Due to that nice property, Equation 27 can be calculated according to Equation 32.
| (31) |
Ga|=y| becomes UDVTa|=y|. Which results in Equation 32
| (32) |
With uniform arguments xi−xj= (j−i)h for all i,j→=
t=0…N and orthogonal polynomials GGT
can be diagonalized and therefore the equation can be easier solved. An example can be found in
subsubsection 6.3.6
| (33) |
with t=
=
=nCr(k,i)
pk,N can now with gk be put in the design matrix and the product GTG will be a (m+ 1) × (m+ 1) Diagonal matrix. Afterwards a can be calculated with the knows formula GTGa=GTy.
From Equation 33 one knows that N(i) and t(i) are the following:
| (34) |
| (35) |
Compute a linear least-squares approximating parabola for the "second window" of five consecutive points (starting with x = 2) in the data.
Lets also say the following:
Note: Normally: m≪N (The degree is smaller than the number of points)
Write down the design matrix and the system of normal equations.
| (36) |
With Equation 30 we get the system of normal equations as one can see in Equation 37:
| (37) |
When one wants to increase the stability of the matrix one can make a statistical normalization.
Compute the output y and the derivative (!) of the approximation at the central coordinate (x = 4)
Apply the filter formulas developed in the exercise before for the data to compute approximately y for x= 3,…,8
Solve subsubsection 6.3.4 again by using the orthogonal polynomials k=0,…,2
From Equation 33 and subsubsection 6.3.3 one knows the three basis functions:
Now we fist have to find a transformation. The transformation can be written in the follwoing way:
| (38) |
With Equation 30 we get the system of normal equations as one can see in Equation 39:
| (39) |
When we now calculate (GTG)−1 ·y one gets The result is therefore:
Which is the same as inparagraph 6.3.4.
Examine and compute a least-squares approximative quadratic parabola for the data
with respect to the basis functions in the following sense:
Compute the design matrix G and the normal matrix. Hint: The normal matrix here is diagonal!
| (40) |
| (41) |
Solve the system of normal equations and write down a formula for the approximating parabola.
divide first row by factor 5.
Also divide other rows by its factor.
What are the dimensions of the unitary matrices U,V , as well as the diagonal matrix D, in the singular value decomposition G=UDVtr
What are the entries (singular values) in the matrix D from above
The singular values are the square-root of the non zero eigenvalues of GT· G and therefore {;
;
}
Give three orthogonal basis polynomials (with respect to the data given) as formulas in the variable
x.
is orthogonal because GT· G is diagonal.
Approximate a continuous polynomial by a Chebyshev polynomial.
Chebyshev Polynomials are defined as Tn(x) = cos(n arccos(x)) with (n= 0,1,…) and (−1 ≤x≤ 1). Due to that, most data points are at the edge. The first polynomials can be found in Equation 42.
| (42) |
Further polynomials can be calculated with the recursion formula Tn+1(x) = 2xTn(x) −Tn−1(n≥ 2) with the initial conditions T1(x) =x,T0(x) = 1.
For Chebychev we use not g but Tx as function.
The matrix GTG can be callculated accroding to Equation 43.
| (43) |
And results then in the follwing matrix
Recipe
Goal: y(t) =pN(t) (define polynomial in [a,b] ) with Chebyshev-polynomials of degree m.
1. transform y(t) on the standard interval [−1,1] (affine Transformation) t=a+(x+ 1).
2. describe y(x) with Tn terms
3. truncate y(x) on degree m : ym(x)
4. back transformation: x= 2
− 1
5. insert Tn in ym see Equation 42
6. error estimation for truncate Method:
maxt( removed part)
Example Approximation of y(t) =t3 with degree m= 2 for the interval (a,b) = (0,1)
A weight function w(x) is often called the function inside the integral, in the case of the formula below
w(x) =.
| (44) |
Equation 44 is true because the polynomial is orthogonal!
Example:Chebyshev continuous least-squares parabola on the interval [0,1] for y(t) =t3 First the interval [0,1] is transformed to [−1,1] by x= 2t− 1 This is shown with ??
In our case our new x is called t. Therefore x= 2t− 1 ⇒t= ⇒y(t) =
Now we can use Equation 45 and
get the following results:
| (45) |
Legendre Polynomials: The Legendre polynomials are defined by the Rodriguez formula which can be seen in Equation 46
| (46) |
Where the first polynomials can be seen in Equation 47
| (47) |
Continuous Legendre least-squares approximation
If y(x) is function on [−1,1] which is absolutely square-integrable with respect to the weight function
w(x) = 1 (x∈ [−1,1]) in the sense that ∫
−11|y(x)|2dx<∞, then the continuous square-sum of residuals in
Equation 48
| (48) |
Is minimal when the coefficients a have the value given in Equation 49. This equation also describes the resulting polynomial.
| (49) |
where m is the degree.
Legendre continuous least-squares parabola on the interval t∈ [0,1] for y(t) =t3.
First one has to do a transformation to the interval x∈ [−1,1]. This results in the following: x= 2t− 1 ⇒t=,
therefore y(x) =
. With Equation 49 one gets then the following:
Note: the degree of a multi-variate polynomial can be identified by adding up the degrees of the variables in each of the terms. It does not matter that there are different variables. The largest number is the degree.
Degree 3.
Degree 4.
Residuals: ri=zi−f (xi) ⇒∑r i2 →min!
Normally, a set of four 3d-points (x,y,z) is not contained in one single plane. But generally there is a plane coming
close to the 3d-points in the sense of least-squares approximation.
The (x,y,z)-data in this problem is: A = (1,0,0), B = (0,1,0), C = (0,2,-1), D = (1,3,1)
Express x3,x4 as linear combinations of the Chebyshev polynomials T0(x),T1(x),T2(x),T3(x),T4(x).
From Equation 42 one knows that T3(x) = 4x3 − 3x⇒T3(x) =x3 −
x⇒
T3(x) +
T1(x) =x3
From Equation 42 one knows that T4(x) = 8x4−8x2+1 ⇒T4(x) =x4−x2+
⇒
T4(x)+
T2(x) =x4−
⇒
T4(x) +
T2(x) +
T0 =x4
Express x3 as linear combinations of the Legendre polynomials P0(x),P1(x),P2(x),P3(x).
From Equation 47 one knows that P3(x) =⇒
P3(x) =x3 −
x⇒
P3(x) +
P1(x) =x3
Compute continuously approximating least-squares lines for the model function y(t) =t2 (0 ≥t≥ 1) by
| (50) |
The purpose of differential is to measure error propagation. (How much is y(dependent variable) wrong when
x(independent variable) is wrong by a certain amount). The differential df is the linear amount of change between
a variable and a function, as it can be seen in Equation 51. Whereby ∆f is the hole amount of change,
not only the linear one (The difference between two points). For small dx on can say ∆f ≈df and
≈
.
| (51) |
As one has seen before, ∆f ≈df for small dx and one has used only the linear part. To further improve the approximation one could not only use the linear part (first derivative) but also the squared (second derivative) and so on. Therefore, a function at a certain point can be approximated by it’s derivates at this point, which is called Taylor series approximation, which can be seen in Equation 52 for the one dimensional case and in Equation 53 for the multidimensional case.
| (52) |
The vector field of of the partial derivative is called gradient of f and is denoted with grad(f ) or ∇f (x). Therefore
∆f ≈∇f (x) ·h. Equation 53 shows the taylor series approximation for the multi-indices α= and
|α|=α1 +…+αn.
| (53) |
The remainder terms Rα are absolutely bounded by maxx∈S
with |α|=N+ 1 and
S=x0 +
is a n-dimensional ’rectangle’ with center x0. (This idea can be used
afterwards by the Jacobian matrix and the determinant)
The formulas for up to order four can be found in Equation 54
| (54) |
The bivariate symmetric (!) function f (x,y) =e− has to be approximated by a bivariate Taylor polynomial of
order 4 around (0,0) by
In the Taylor series approximation for multi-indices, one has seen that ∆f ≈∇f (x) ·h for small dx (see also
Equation 53). When one writes all those gradients in one matrix, one gets the so-called Jacobian matrix. Which
actually tells us the same as mentioned in subsubsection 7.1.1, but just for a multivariable problem. It tells us how
y1,y2,… (dependent variable) changes when, x1,x2,… (independent variable) changes. Furthermore it has the nice
property that the determinant of this matrix also describes how the volume changes when one changes a certain
variable.Therefore the Matrix can be used to analyse the error propagation or make volume calculation in a
different coordinate system.
Below one can find some definitions.
| (55) |
| (56) |
| (57) |
In the special case that n = m the Jacobian matrix is a square matrix and thus has a determinant (called Jacobian determinant):
| (58) |
| (59) |
Lets assume one measures an angle (α,γ) and want the position (x,y). Let’s call the transformation from (α,γ) to (x,y) T and from (x,y) to (α,γ) T−1
To solve this problem one can follow the following approach:
The formulas x=r cos(φ), y=r sin(φ) (0 <r, 0 ≤φ< 2π) define the coordinate transform T from polar
coordinates (r,ϕ) to Cartesian coordinates (x,y) in the punctured plane R2' {(0,0)}.
Compute the Jacobian matrix JT(r,φ) and its Jacobian (determinant) detJT(r,φ) as well as the Jacobians
(determinants) detJT(x,y),detJT−1(r,φ) and detJT−1(x,y)
First of all one has to write down the transformations
Once one has done that one can calculate the Jacobian Matrix:
and afterwards the determinant
when one wants to express r in x and y one knows that r= therefore
and
Elliptical coordinates (σ,τ) (σ> 1,−1 <τ< 1) for a = 1 are connected to Cartesian coordinates (x, y) through the transforming formulas:
Compute the Jacobian matrix
Express the Jacobian determinant
Express the Jacobian determinant in x, y, since the denumerator is exactly y, we know it already. Furthermore the
following is true: =σ2 −τ2
An ODE is a differential equation where it’s derivatives belong to only one variable. Furthermore it is possible that
an ODE can not be solved explicitly, due to that in this chapter it will be investigated how they can be solved
numerically.
A first order differential value problem can be expressed like the one in Equation 60
| (60) |
One way to solve the problem numerically is by tailor series approximation, as it can be seen in Equation 61. (Remember that the tailor series is evaluated from one single point). The idea is that one creates a tailor series approximation up to order p at the starting point and moves then with a step size h to the new position one got from the tailor series approximation and does there the same until one reaches the destination.
(61) |
The calculations up to order three (p=3) are given in Equation 62:
| (62) |
The Euler method is a special case of the explicit methods where p= 1 and h=const. The Formulas to calculate it can be found in Equation 63.
| (63) |
Global Error:
| (64) |
Local Error:
| (65) |
Local slope Error:
| (66) |
Solve the initial value problem y′=xy1/3 with y(1) = 1 numerically by the method of Taylor with order p = 4 and fixed step-size h = 0.1 for the x-values 1.1 and 1.2 (two steps). All final (!) results should be rounded to the 10th digit. Furthermore, compute the local error (slope) as well as the global error for the two steps. Note that the exact solution of the equation is given by Equation 67.
| (67) |
To find out x at 1.1 one firstly needs to calculate the it’s tailor series approximation at the starting
point.
With Equation 61 one can then write down the following:
Then one does the same at the new location on got from the previous result.
The global error is defined by Equation 64 and therefore has the following result:
The local error is defined by Equation 66 and therefore has the following result:
and for n=1 one has the following result:
Since the calculation of the tailor approximation series is quite tedious. One came up with another method, which is recursive and results in the same as the tailor series approximation (big advantage is that no computations of derivatives up to order p are needed). In Equation 68 one can find the Common Runge-Kutta method of order 4. As one can see there one has seven variables, when one now sets this equal with the tailor series approximation all those variables are defined in the end as it can be seen in Equation 69.
| (68) |
| (69) |
For the classic runge-kutta method one can also write Equation 70 which results in Equation 71.
| (70) |
| (71) |
The errors are calculated nearly the same way as in the previous section. Equation 74.
Global Error:
| (72) |
Local Error:
| (73) |
When there is only one step calculated, the local error must be the same as the global error.
Local slope Error:
| (74) |
Solve the initial value problem y′=xy1/3 y(1) = 1 numerically by the classical Runge-Kutta method of order p = 4
and fixed step-size h = 0.1 for the x-values 1.1 und 1.2 (two steps). All final (!) results should be rounded to the 10th
digit. The exact solution of the equation is y=3/2.
From Equation 71 one knows that:
As one can see, the result is nearly the same as in the previous Example. The local slope error can be calculated according to Equation 74.
The local error can be calculated according to Equation 73 and results in the following:
The Butcher tableau is mainly a mnemonic device (Gedächtnissstütze) to remember the coefficients. The tableau must fullfill the condition listed in Equation 75
| (75) |
Where the variables mean the folwoing:
The general tableau can be seen in Equation 76.
| (76) |
A step from xn to xn+1 =xn+hn(n= 0,1,… ) in the general Runge-Kutta method is defined by Equation 77 where the values a,b,c can be read from the butcher tableau.
| (77) |
Some examples for butcher tableaus can be found in Table 1
The simplest adaptive Runge–Kutta method involves combining Heun’s method, which is order 2, with the Euler method, which is order 1 (also called Heun-Euler 2(1)). Its extended Butcher Tableau can be seen in Equation 78.
| (78) |
The Idea is to automatically adapt the step-size h. Due to that one needs a new way to define the approximation of the error, which can be done with an Accuracy Goal (ac), which defines how many decimal places (Nachkommastellen) are correct and a precision Goal (pg), which represents the significant digits of the result. The two parameters are considered in the tolerance parameter, ε which can be found in Equation 79.
| (79) |
Furthermore, one needs a second approximation for the error calculation, with the order ˆ p. The first order approximation p is needed to calculate the step size. Mostly ˆ p=p− 1. Due to that the butcher tableau is extended by a row (b values) as it can be seen in Table 2.
| 0 | 0 | 0 | | 0 | 0 |
| c 2 | a2,1 | 0 | | 0 | 0 |
| | | | | 0 | |
| cs−1 | as−1,1 | as−1,2 | | 0 | 0 |
| cs | as,1 | as,2 | | as,s−1 | 0 |
| b1 | b2 | | bs−1 | bs | |
| ˆ b1 | ˆ b2 | | ˆ bs−1 | ˆ bs | |
The local error can be calculated according to Equation 80.
| (80) |
Below one can find again a short description of the variables:
To know if the step size is good or not one calculates . When the current step
> 1, then the estimation of
hn was too optimistic and the step must be repeated with a smaller step size. One also says the current step is
Rejected. Otherwise when
≤ 1 the step size is ok and one can proceed. Updating the step size is done according
to Equation 81.
| (81) |
ε=εa+εr with ˜ p= min(p, ˆp) + 1 (order of the primary method)
The global relative error must not diverge, which means it must be limited. Since it is difficult to make a statement about the analysed ODE one uses benchmark equations. One of the most commonly used ones is the Dahlquist model, which can be seen in Equation 82
| (82) |
The solution of this equation is y=eℜ{A}x, which is an oscillation with a exponential
amplitude eℜ{A}x and frequency ℑ{A}. The
The exact solution is: Y(x) =e−λx Consider Euler’s method: Solation will go to zero iff
Stability for heun-method (rk-2)
From Equation 77 one knows that yk+1 =yk+h· ( ·k1 +
·k2)
| (83) |
From that one can somehow derive three cases which are listed below
The stability condition for case one can know be calculated as the following (ℜ{A}< 0) and
1 >|F(z)|=⇒−2 <hℜ{A}< 0. since x1,2 =
=
=−1 ± 1 and therefore
the values must be between 0 and -2. The stability polynomial in this exercise was F(z) = 1 +z+
(z=hA).
Recursive Formulas
For the stability polynomials in the form: F(z) = 1 +b1k1(z) +…+bsks(z) recursive equations exist as can be seen in
Equation 84.
| (84) |
Solve the initial value problem φ′=c(1 −εcosφ)2 φ(0) = 0 with c= 1 and ϵ= 0.25 numerically by applying the
Heun-Euler 2(1) embedded adaptive method with classical step-size control until 3 proceeding steps
are executed. The initial step-size equals 0.001, the accuracy goal (ag) 4 and the precision goal is 4 ,
either.
Create a table listing values for , state ) containing at least three preceding
steps.
According to the exercise, we know the following:
| x | y | hn | ek | | hn+1 | state |
| 0 | 0 | 0.001 | 2.966 · 10−11 | 1.836 · 103 | 1.836 | Proceed |
| 0.001 | 0.0005625 | 1.836 | 0.18169 | 0.02347 | 0.043 | Reject |
Using Theorem 1.3 in the script (p. 29) gain the A-stability polynomial F1(z) = 1 +z+ +
for the embedded
adaptive method SS3(2) with Butcher tableau.
From Equation 84 one knows that a stability polynomial is of the form F(z) = 1+b1k1(z)+b2k2(z)+b3k3(z)+0k4(z), whereas:
The stiffnes is dependent on:
Stiffness Detection
Heun euler does not work when we have stiffness situations. Condition: cs−1 =cs= 1. Through testing of
to the absolute borders of the stability region the stiffness can be detected. Stiffness is present when |h˜λ| is outside
or at the border of the stability condition.
Example for explicit runge-kutta
˜λ is an estimation for fy=f (x,y) for example y′=x4 − 25y4 =f (x,y) and takes the role of ℜ{A} for the
stability analysis.
Given the differential equation y′=f (x,y) y(0) = 4 carry out a stiffness detection test using the
A-stability region and the partial derivative fy at the initial values and step size h= 1. The method is defined by the
Butcher tableau below.
The exercise can be solved in two steps:
To calculate the stability region one hast to set the stability polynomial to zero and therefore one gets:
x1,2 ==
=−1 ± 1 and therefore the boundary is -2 and 0.
Solve the van-der-Pol ODE-system z(0) = 1,v(0) =−1, µ= 0.2 numerically by applying
the Heun-Euler 2(1) embedded adaptive method with classical step-size control until 3 proceeding steps are
executed. The initial step-size equals 0.001, the accuracy goal (ag) 1 and the precision goal is 2. Create a
table listing values for
state) containing at least three proceeding
steps.
According to the exercise, we know the following:
Therefore ek= 0.001 · (− ·
+
·
) =
| x | y | hn | ek | | hn+1 | state |
| 0 | | 0.001 | | 469.04157598235 | 0.46904 | Proceed |
| 0.001 | | 0.46904157598235 | Reject | |||
| (85) |
| (86) |
| (87) |
| (88) |
| (89) |
Where
| Degrees | 0◦ | 30◦ | 45◦ | 60◦ | 90◦ |
| Radians | 0 | | | | |
| sin 𝜃 | 0 | | | | 1 |
| cos 𝜃 | 1 | | | | 0 |
| tan 𝜃 | 0 | | 1 | |
| cotx | = | ||
| cscx | = | ||
| secx | = |
| sin(−x) | =−sinx | ||
| cos(−x) | = cosx | ||
| tan(−x) | =−tanx |
| sin2x+ cos2x | = 1 | ||
| 1 + tan2x | = sec2x | ||
| 1 + cot2x | = csc2x |
| sin( | = cosx | ||
| cos( | = sinx | ||
| tan( | = cotx | ||
| cot( | = tanx | ||
| sec( | = cscx | ||
| csc( | = secx |
| sin(x+y) | = sinx cosy+ cosx siny | ||
| sin(x−y) | = sinx cosy− cosx siny | ||
| cos(x+y) | = cosx cosy− sinx siny | ||
| cos(x−y) | = cosx cosy+ sinx siny | ||
| tan(x+y) | = | ||
| tan(x−y) | = |
| sin(2x) | = 2sinx cosx | ||
| cos(2x) | = cos2x− sin2x | ||
| = 2cos2x− 1 | |||
| = 1 − 2sin2x | |||
| tan(2x) | = |
| sin | =± | ||
| cos | =± | ||
| tan | = | ||
| = |
| sin2x | = | ||
| cos2x | = | ||
| tan2x | = |
| sinx siny | = | ||
| cosx cosy | = | ||
| sinx cosy | = | ||
| tanx tany | = | ||
| tanx coty | = |
| sinx+ siny | = 2sin | ||
| sinx− siny | = 2cos | ||
| cosx+ cosy | = 2cos | ||
| cosx− cosy | =−2sin | ||
| tanx+ tany | = | ||
| tanx− tany | = | ||
1. =
±
2.
=k·
(k konstant )
3.
=
·v+u·
4.
=
5.
=
·
falls z=f (y) und y=g(x)
6.
=nxn−1
7.
= ex
8.
=axlna (a> 0)
9.
(lnx) =
10.
(sinx) = cosx
11.
(cosx) =−sinx
12.
(tanx) =
13.
(arcsinx) =
14.
(arctanx) =
1. ∫
ab(u±v)dx=∫
abu dx±∫
abv dx
2. ∫
abk·u dx=k∫
abu dx (k konstant )
3. ∫
x=abf (g(x))g′(x)dx=∫
w=g(a)g(b)f (w)dw
4. ∫
abu· dx=
ab−∫
ab
·v dx
1. ∫
xn dx=xn+1 +C,n≠− 1
2. ∫
dx= ln|x|+C
3. ∫
ax dx=
ax+C,a> 0
4. ∫
lnx dx=x lnx−x+C
5. ∫
sinx dx=−cosx+C
6. ∫
cosx dx= sinx+C
7. ∫
tanx dx=−ln|cosx|+C
Development of f around a
in which k! = 1 · 2 · 3 ·…·k.
The last three only converge for |x|< 1.
| (90) |