Blog

Semiconductors (This are just some notes I took)

1. Introduction to Semiconductor Physics

Semiconductors are the foundation of modern electronics. To truly understand how these materials work and why they’re so important, we need to delve into the quantum mechanical principles that govern their behavior. This article will take you on a journey from the fundamental concepts of quantum mechanics to the practical applications in semiconductor devices.

2. Fundamental Concepts of Quantum Mechanics

2.1 The Uncertainty Principle

At the heart of quantum mechanics lies Heisenberg’s Uncertainty Principle. This principle states that we cannot simultaneously know both the position and momentum of a particle with absolute precision. Mathematically, this is expressed as:

    \[\Delta x \cdot \Delta p \geq \frac{\hbar}{2}\]

Where \Delta x is the uncertainty in position, \Delta p is the uncertainty in momentum, and \hbar is the reduced Planck constant.

Similarly, there’s an energy-time uncertainty relation:

    \[\Delta E \cdot \Delta t \geq \frac{\hbar}{2}\]

These principles are fundamental to understanding the behavior of particles at the quantum scale.

2.2 Wave-Particle Duality

Another key concept is the wave-particle duality, encapsulated in the de Broglie relation:

    \[\lambda = \frac{h}{p}\]

This equation relates the wavelength \lambda of a particle to its momentum p, with h being Planck’s constant. This duality means that particles can exhibit wave-like properties, and waves can exhibit particle-like properties.

2.3 The Wave Function

In quantum mechanics, particles are described by wave functions, usually denoted as \psi(x,t). The probability of finding a particle at a particular position and time is given by the square of the absolute value of the wave function:

    \[P(x,t) = |\psi(x,t)|^2\]

3. The Schrödinger Equation

The cornerstone of quantum mechanics is the Schrödinger equation. In its time-independent form for a one-dimensional system, it’s written as:

    \[-\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + V(x)\psi = E\psi\]

Where m is the mass of the particle, V(x) is the potential energy, and E is the total energy.

For many systems, this equation can be simplified to:

    \[\frac{d^2\psi}{dx^2} = -k^2\psi\]

Where k is the wave number, related to the particle’s energy and mass by:

    \[k = \sqrt{\frac{2mE}{\hbar^2}}\]

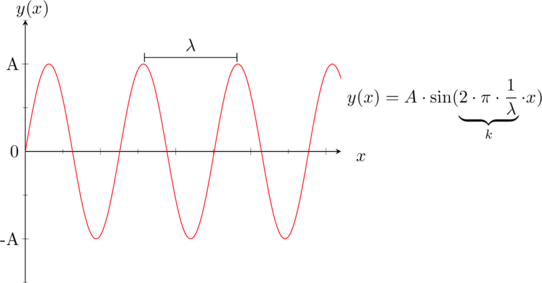
The solutions to this equation are sinusoidal functions, which form the basis for understanding electron behavior in semiconductors.

Rendered by QuickLaTeX.com

 In quantum mechanics, k does directly relate to the momentum of the particle p=\hbar \cdot k. From standard physics we know equation 1

(1)   \begin{equation*} E=\frac{p^2}{2m} \end{equation*}

When inserting equation ?? in equation 1 We get equation 2 and when we rearrange everything equation 3.

(2)   \begin{equation*} E=\frac{\left(\frac{h}{\lambda}\right)^2}{2 m} \end{equation*}

(3)   \begin{equation*} \lambda^2=\frac{h^2}{2 m E} \end{equation*}

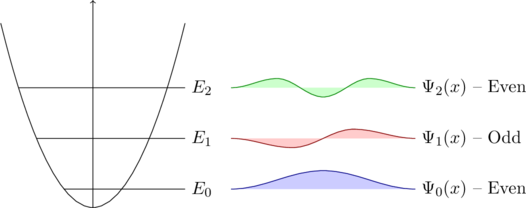
Furthermore we know from the figure above that k=\frac{2 \cdot \pi}{\lambda} When we insert this in equation 3 we get after some rearinging equation 6 which is the same as equation ??. 0.0.1. Infinite Potential WellNow we want to find a solution to the differential equation. Let’s assume we have a cube of silicon. The electrons are for sure inside this cube/lattice. So the probability that they are outside of the latice is zero. This behaviour can also be described with the graphic below: C

Rendered by QuickLaTeX.com

} For the condition of a solution of the differential equation one can say that the probability of finding an electron must be zero at both ends, therefore the only solution would be a sine (see the possible solutions for the differential equation).

    \[\Psi_0(x)=A_1\sin(k\cdot x)\]

Furthermore we now that A_1\sin(k\cdot L)=0 therefore k\cdot L = n \cdot \pi \Rightarrow k = \frac{n \cdot \pi}{L}. So therefore k can only take certain values, which means the energy is restricted to certain values. The last thing that remains now is to solve for A_1. We further know equation 4, which says integral of the probability of the particle must be one.

(4)   \begin{equation*} \int_{-\infty}^{\infty}|\Psi|^2 d x=1 \end{equation*}

Therefore we end up with the following:

(5)   \begin{equation*} \begin{gathered} \int_0^L A_1^2 \sin ^2(k x) d x=1 \\ A_1=\sqrt{\frac{2}{L}} \end{gathered} \end{equation*}

Rendered by QuickLaTeX.com

(6)   \begin{equation*} k^2=\frac{2 m E}{\hbar^2} \end{equation*}

link to sphere

(7)   \begin{equation*} \begin{array}{r} n=\int \underbrace{g(E)}_{\text {density of states}} \cdot \underbrace{P(E)}_{\text { Probability state is occupied }} d E} \end{array} \end{equation*}

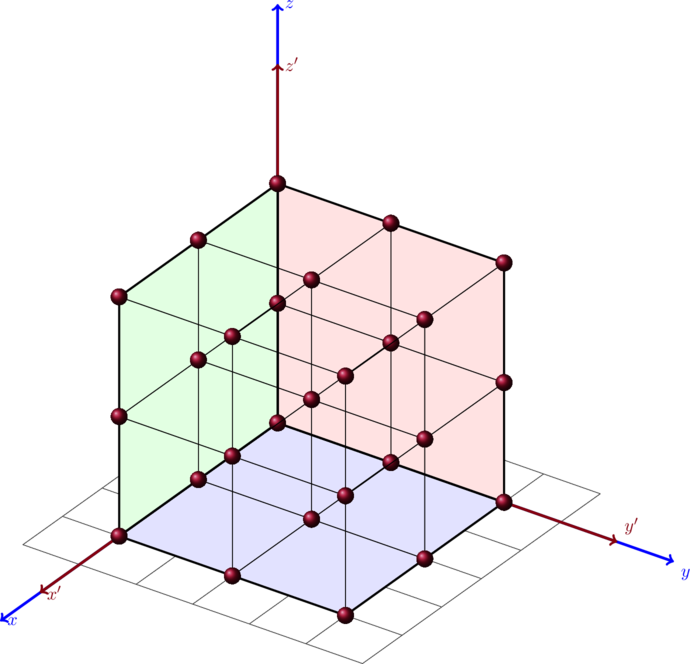
Now want to calculate g(E). To do that we have to calculate the total number of states divided by the total volume of the semiconductor.

(8)   \begin{equation*} g(E)=\frac{N}{L^3} \end{equation*}

Rendered by QuickLaTeX.com

 Assuming that the apples are equally spaced as in the plot above one can say that eacht apple is in a distance to the other with a distance of a. The density apple per volume is in this case \frac{1}{a^3} which is one apple per a^3. The total number of apples is know the volume divided by the apple density

    \[N=\frac{V}{\frac{1}{a^3}}\]

The volume of a spherical shell is 4\cdot \pi \cdot r^2 \Delta \r. From before we know that the states of an electron are defined like the following: k=\frac{\pi}{L}\cdot n therefore the states are in a distance to each other of \frac{\pi}{L}. Futher more we can say that we have a state volume, therefore r^2 in this volume is just k^2 which is k_x^2+k_y^2+k_z^2 and therefore

    \[N=\frac{4 \cdot \pi \cdot k^2 \cdot \Delta k}{(\frac{\pi}{L})^3}\]

When we only take the positive k_x, k_y, k_z direction we also get a factor of \frac{1}{8}. The density of states in a certain volume is then given by the following formula:

    \[\frac{N}{L^3}=\frac{1}{8}\cdot\frac{4 \cdot k^2 \cdot \Delta k}{(\pi^2}\]

Now we want to substitute dk with dE. We already know:

    \[\begin{aligned} k &=\sqrt{\frac{2 m E}{\hbar^2}} \\ \frac{dk}{d E} &=\frac{1}{2} \sqrt{\frac{2 m}{\hbar^2 E}} \\ d k &=\frac{1}{2} \sqrt{\frac{2 m}{\hbar^2} \frac{1}{E}} d E \end{aligned}\]

With this information we can then replace k in the original equation which results in the following:

    \[\begin{aligned} &\frac{4 \cdot \frac{2 m E}{\hbar^2} \frac{1}{2} \sqrt{\frac{2 m}{\hbar^2} \frac{1}{E}} d E}{8 \pi^2} \\ &g(E) d E=\frac{2 \pi(2 m)^{3 / 2}}{n^3} \sqrt{E} d E \end{aligned}\]

And because an electron can have an up and down spin we get the following:

    \[&g(E) d E=2 \cdot \frac{2 \pi(2 m)^{3 / 2}}{n^3} \sqrt{E} d E\]

    \[\frac{-\hbar^2}{2 m} \frac{\partial^2 \Psi}{\partial x^2}=i \hbar \frac{\partial \Psi}{\partial t}\]

or 1. intrinsic & extrinsic semiconductors Where p-type and n-type materials meet is called a p-n junction. Electrons from the n-type material move to the p-type material and close the holes and vice versa. This is called \textbf{diffusion} and leads to a {depletion layer} In an n-channel mosfet the inversion is called inversion because the p-type material looks like n-type.

Leave a Reply